1319. Дуэлянты

«Среди долины ровныя...». 1883. «Среди долины ровныя...» — классическое произведение Шишкина. Художник порой увлекался передачей поэтических мотивов, которые он видел в природе. Так, следуя некогда популярной песне А.Ф. Мерзлякова, в этой картине он пытался выразить величие могучего одинокого дуба, возвышавшегося среди широты полей.

Среди долины ровныя,
На гладкой высоте,
Цветет, растет высокий дуб
В могучей красоте.

Высокий дуб развесистый,
Один у всех в глазах;
Один, один, бедняжечка,
Как рекрут на часах!
Взойдет ли красно солнышко -
Кого под сень принять?
Ударит ли погодушка -
Кто будет защищать?
Ах, скучно одинокому
И дереву расти!
Ах, горько, горько молодцу
Без милой жизнь вести!

Среди долины ровныя Петр Иванович и Илья Васильевич решили выяснить отношения на дуэли. Но никому из них не хотелось умирать. Поэтому они договорились, что каждый из них прибывает к дубу (место встречи) в случайный момент времени между 5 и 6 часами утра и, прождав соперника n минут, удаляется. В случае прибытия последнего в эти n минут дуэль состоится. Вычислить вероятность того, что дуэль закончится поединком.

Вход. Каждая строка является отдельным тестом и содержит целочисленное значение n (0 < n ≤ 60).

Выход. Для каждого теста в отдельной строке вывести вероятность того, что дуэль закончится поединком. Результат выводить с точностью до 6 десятичных знаков.

Пример входа

5

50

60

Пример выхода

0.159722

0.972222

1.000000

РЕШЕНИЕ

теория вероятности

Анализ алгоритма

Пусть x и y обозначают время прибытия первого и второго дуэлянтов соответственно, измеренное в долях часа, начиная с 5 часов. Заштрихованная площадь квадрата отвечает случаю, когда дуэлянты встречаются для случая n = 5 минут = 1/12 часа. Вероятность того, что дуэлянты не встретятся, равна

(сумма площадей двух треугольников)

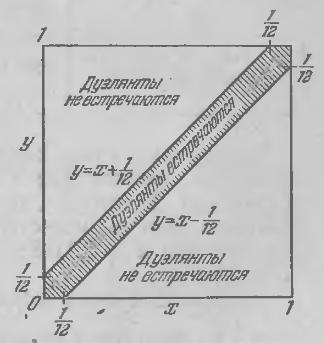
Соответственно вероятность поединка составляет .

Реализация алгоритма

Читаем входные данные, вычисляем искомую вероятность поединка и выводим ее.

while(scanf("%lf",&n) == 1)

{

res = 1 - (1.0-n/60.0)*(1.0-n/60.0);

printf("%.6lf\n",res);

}